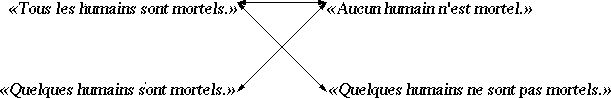La logique est l'ensemble des relations conditionnelles que des représentations puissent représenter une réalité.

La logique est l'ensemble des relations conditionnelles nécessaires de vérité ou de fausseté entre des assertions.

Par exemple, s'il est vrai qu'il pleut, il est nécessairement faux qu'il ne pleut pas; s'il est vrai qu'il existe réellement un arbre qui ne perd pas ses feuilles en hiver, il est nécessairement faux que tous les arbres perdent leurs feuilles en hiver; s'il est vrai que je suis un humain et que tous les humains sont mortels, il est nécessairement vrai que je suis mortel; s'il est vrai que je ne fume plus, il est nécessairement vrai que j'ai déjà fumé.

*

Est logique une relation entre des représentations telle que la réalité de ce que représente l'une implique la réalité de ce que représente l'autre .

La logicité est le fait que la réalité de ce que représente une représentation implique la réalité de ce que représente une autre représentation.

Par exemple, il est logique qu'il soit vrai que je cesse de fumer et qu'il soit vrai que je fumais.

Est illogique une relation entre des représentions telle que la réalité de ce que représente l'une implique l'irréalité de ce que représente l'autre.

L'illogicité est le fait que la réalité de ce que représente une représentation implique l'irréalité de ce que représente une autre représentation.

Par exemple, il est illogique qu'il soit vrai qu'il pleuve et qu'il soit vrai qu'il ne pleuve pas.

Est alogique une relation entre des représentions telle que la réalité de ce que représente l'une n'implique ni la réalité ni l'irréalité de ce que représente l'autre.

L'alogicité est le fait que la réalité de ce que représente une représentation n'implique pas la réalité de ce que représente une autre représentation.

Par exemple, il est alogique qu'il soit vrai qu'il pleuve et qu'il soit vrai que j'aie pris un parapluie.

La déduction est une inférence logique, pas l'induction ni l'abduction qui sont des inférences alogiques.

*

Une contradiction est la production d'une représentation telle qu'elle/qui fait partie d'un ensemble de représentations tel que le fait qu'une ou plusieurs de ces représentations représentent une réalité implique qu'une de ces représentations ne représente pas une réalité.

Une contradiction est une relation entre des représentations telle que le fait qu'une ou plusieurs représentent une réalité implique qu'une représentation ne représente pas une réalité.

Par exemple, «`Il pleut.'» et «`Il ne pleut pas.'» sont contradictoires.

«`Prends ton parapluie.'» et «`Ne prends pas ton parapluie.'» sont contradictoires.

«`Je te maudis.'» et «`Je te bénis.'» sont contradictoires.

«Tout est bleu.» est contradictoire avec «Tout n'est pas bleu.» (contraire) et avec «Rien n'est bleu.» (opposé), mais «Tout n'est pas bleu.» et «Rien n'est bleu.» ne sont pas contradictoires (d'ailleurs, la vérité de «Rien n'est bleu.» implique la vérité de «Tout n'est pas bleu.»).

«`Je te promets de venir.'» contredit «`Je ne te promets pas de venir.'» et «`Je te promets de ne pas venir.'» (mais «`Je ne te promets pas de venir.'» et «`Je te promets de ne pas venir.'» ne sont pas contradictoires).

«Il ne fume plus.» (ou «Il a cessé de fumer.») et «Il n'a jamais fumé.» sont contradictoires, car qu'il ne fume plus implique qu'il a déjà fumé, et donc qu'il est faux qu'il n'a jamais fumé.

Entre «J'ai l'intention de me marier en juin.» dit en avril et «Je n'ai pas l'intention de me marier en juin.» dit en mai, il n'y a pas contradiction, alors qu'il y a contradiction entre «Je me marierai en juin.» dit en avril et «Je ne me marierai pas en juin.» dit en mai.

Si «Mon ballon est vert.» et «Mon ballon est bleu.» ne sont pas contradictoires, elles le deviennent avec l'assertion «Mon ballon est monochrome.»

L'affirmation «Cette phrase ne comporte pas sept mots", qui comporte sept mots, est donc fausse; comme sa négation, «Cette phrase comporte sept mots»: elles ne sont donc pas contradictoires.

Les affirmations "Le roi de France s'est absenté hier." et "Le roi de France ne s'est pas absenté hier." sont toutes les deux fausses, car il n'y a plus de roi de France (présupposé faux).

Schéma où les traits représentent les relations de contradiction entre les énonciations:

*

Un syllogisme est un ensemble de trois assertions dont la vérité de deux implique la vérité de l'autre (de la troisième).

Par exemple, la vérité de «Tous les mammifères sont des animaux.» et de «Tous les humains sont des mammifères.» implique la vérité de «Tous les humains sont des animaux.».

Un enthymème est un syllogisme réduit à deux assertions, l'assertion intermédiaire (la deuxième) étant sous-entendue.

Un enthymème une formulation partielle d'un syllogisme dans laquelle on sous-entend l'une des deux prémisses ou la conclusion.

Par exemple, «Je suis un humain.» peut sous-entendre: «Or tous les humains sont sujets à l'erreur; donc je suis sujet à l'erreur.».

Par exemple, «Je pense, donc je suis.» est un enthymème où est sous-entendu que tout ce qui pense est.

*

Un jugement est une conclusion de la vérité, de la réalité, de la fausseté ou de l'irréalité de quelque chose.

*

Démontrer, c'est prouver la vérité (réelle ou conditionnelle) de la conclusion, par des déductions à partir de prémisses vraies.

Une démonstration est une déduction prouvant la vérité de la conclusion à partir de prémisses vraies.

Une démonstration est la preuve de la vérité d'une conclusion, par des déductions à partir de prémisses vraies.

*

Une tautologie est une assertion qui est nécessairement vraie de par sa signification.

Par exemple, «Un chat est un chat.», «Un égale un.», «Un sou est un sou», «Un ordre est un ordre.», «Dieu est Dieu, nom de Dieu», «Quand il a une idée dans la tête, il ne l'a pas dans les pieds.», «L'Homme énergique et qui réussit, c'est celui qui parvient à transformer en réalités les fantaisies du désir» (Sigmund Freud) sont des tautologies.

Une antilogie est une assertion qui est nécessairement fausse de par sa signification.

Par exemple, «Un chat n'est pas un chat.», «Un n'égale pas un.», «Apprendre ce qu'on sait déjà.», «Je sais que je ne sais rien.» sont des antilogies.

Par exemple, «Je n'ai pas vu ce que j'ai vu.» est une antilogie, mais «Selon eux, je n'ai pas vu ce que j'ai vu.» n'est pas une antilogie.

«Tout philosophe a deux philosophies: la sienne et celle de Spinoza.»; si Spinoza a une philosophie, c'est un philosophe; il a donc deux philosophies: la sienne et celle de Spinoza; il n'a donc qu'une unique philosophie; donc tout philosophe n'a pas deux philosophies; donc cette affirmation est une antilogie. L'affirmation «Tout philosophe, sauf Spinoza, a deux philosophies: la sienne et celle de Spinoza.» n'est pas une antilogie.