Relations

Mêmeté, altérité, identité et différence

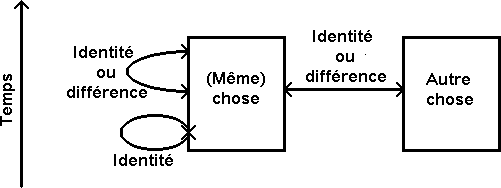
Une (même) chose peut être différente de ce qu'elle était ou de ce qu'elle sera.

Par exemple, je suis la même personne maintenant (adulte) qu'avant (enfant), mais je suis différent de ce que j'étais: plus grand, plus lourd , plus vieux, moins souple, etc.

Je peux me rebaigner dans le même fleuve (par exemple la Garonne) même s'il y a autour de moi d'autres molécules d'eau en contact avec ma peau que lors de ma première baignade et que le fleuve est différent de la première fois où je m'y suis baigné (par exemple il est en crue, son eau est plus polluée, ou son parcours est modifié, etc.).

Une (même) chose ne peut pas être différente d'elle-même (ou est nécessairement identique à elle-même) au même instant.

Soit une chose, une autre chose peut être identique à ou différente de cette chose.

Par exemple, soit une chaise, une autre chaise peut être identique à ou différente de cette chaise.

Si une chose n'existe plus puis est refaite avec les mêmes choses (éléments) qui la faisaient, c'est la même chose.

Par exemple, si je démonte un manège et que je le reconstruis (ici ou ailleurs) avec les mêmes pièces, c'est le même manège.quantité

Si une chose est peu à peu faite avec d'autres choses que celles qui la faisaient, cela reste la même chose.

Par exemple, si je change l'une après l'autre toutes les anciennes pièces d'un bateau par de nouvelles, cela reste le même bateau.

Si une chose est faite avec des choses qui faisaient autre chose, c'est une autre chose que cette autre chose (et la même chose que la première chose).

Par exemple, si avec toutes les anciennes pièces d'un premier bateau, je construis un deuxième bateau, c'est un autre bateau (même s'il est peut-être plus identique au premier bateau tel qu'il était auparavant que celui-ci ne l'est maintenant).

Un changement est une différence à soi-même, ou l'altérité dans ce qu'a, est ou fait une (même) chose.

Par exemple, si un caméléon change de couleur, c'est qu'il est d'une couleur différente à celle qu'il avait; si je change de position, j'ai une position différente de celle que j'avais; si je change de voiture, j'ai une autre voiture que celle que j'avais (même si elle est identique).

*

L'absoluité est pour une chose le fait d'être sans relation avec autre chose.

Par exemple, si je suis plus grand qu'un enfant, et qu'il deviendra plus grand que moi, je serai devenu plus petit que lui, c'est-à-dire relativement plus petit, sans être devenu nécessairement plus petit absolument, c'est-à-dire plus petit que moi-même avant.

Une entité est une chose sans relation, ou en tant qu'elle est sans relation, ou en tant qu'elle n'est pas une relation.

Par exemple, un homme est une entité, un père est une entité en tant qu'homme, mais pas en tant que père: la paternité est une relation, pas une entité.

*

Le nombre est la relation d'accumulation entre des choses identiques.

Par exemple si le nombre de pommes dans un placard est de quatre, celui de poires de trois, et qu'il n'y a pas d'autre fruit, le nombre de fruits dans ce placard est de sept.

La quantité est la relation d'accumulation de la même chose.

Par exemple, la contenance d'une bouteille est la quantité de son espace intérieur.

Le nombre est absolu et la quantité est relative (à une autre unité).

Le nombre est discontinu et la quantité est continue.

Par exemple, il est possible d'avoir exactement trois bouteilles, mais pas exactement trois litres de lait, mais la quantité de lait dépendant d'un nombre de molécules de lait, la quantité de lait ne sera pas précisément continue (mais est-ce que la dilatation et la contraction du lait selon la température rend la quantité continue?).

Par exemple, on compte des bouteilles (0, 1, 2, 3 ou 4...) mais on mesure la quantité de lait qu'elles contiennent (0,83 litre ou 2,71 litres...).

On peut manger un quart de melon, donc un quart (1/4) est un nombre, mais on ne mange pas exactement un quart du melon.

Si le nombre moyen d'enfants par femme est de 1,77, 1,77 est un nombre.

L'égalité est la mêmeté numérique ou quantitative.

L'inégalité est l'altérité numérique ou quantitative.

Par exemple, 1 mile, 1609 mètres et 1,609 kilomètre, c'est la même quantité: 1 mile = 1609 mètres = 1,609 kilomètre.

Contrariété, opposition et inversion.

L'amour de Pierre pour Marie (Pierre aime Marie) a pour contraire le non-amour de Pierre pour Marie (Pierre n'aime pas Marie), pour opposé la haine de Pierre pour Marie (Pierre hait Marie), et pour inverse l'amour de Marie pour Pierre (Marie aime Pierre), pour contraire-opposé la non-haine de Pierre pour Marie (Pierre ne hait pas Marie), pour contraire-inverse le non-amour de Marie pour Pierre (Marie n'aime pas Pierre), pour opposé-inverse la haine de Marie pour Pierre (Marie hait Pierre), et pour contraire-opposé-inverse la non-haine de Marie pour Pierre (Marie ne hait pas Pierre).

La possibilité et l'impossibilité sont contraires.

La mortalité et l'immortalité ne sont pas contraires.

Par exemple, une pierre n'est ni mortelle ni immortelle, car elle n'est pas vivante.

L'opposé implique le contraire (et l'opposé-inverse implique le contraire-inverse).

Par exemple, la haine de Pierre pour Marie (Pierre hait Marie) implique le non-amour de Pierre pour Marie (Pierre n'aime pas Marie) (et la haine de Marie pour Pierre (Marie hait Pierre) implique le non-amour de Marie pour Pierre (Marie n'aime pas Pierre).

La réciprocité est le fait pour une relation qu'il y ait sa relation inverse.

La réciprocité est l'ensemble d'une relation et de la relation inverse.

Par exemple, un amour réciproque est un amour où le sujet aimé est aimé par le sujet qu'il aime.

Les relations de contrariété, d'opposition et d'inversion sont des relations réciproques.

Par exemple, si Pierre aime Marie a pour contraire Pierre n'aime pas Marie, Pierre n'aime pas Marie a pour contraire Pierre aime Marie; si Pierre aime Marie a pour opposé Pierre hait Marie, Pierre hait Marie a pour opposé Pierre aime Marie; si Pierre aime Marie a pour inverse Marie aime Pierre, Marie aime Pierre a pour inverse Pierre aime Marie.

La neutralité est le fait d'être hors d'une opposition.

*

«... Et...» représente la relation entre des choses telle il y ait toutes les choses reliées.

«... Ou...» représente la relation entre des choses telle qu'il y ait au moins une des choses reliées.

«Soit... soit...» représente la relation entre des choses telle qu'il n'y ait qu'une des choses reliées.

«Ni... ni...» représente la relation entre des choses telles qu'il n'y ait aucune des choses reliées.

L'implication est une relation telle que s'il y a la première des choses, il y ait nécessairement la seconde. 

Être (ou avoir ou faire) une chose ou une autre, c'est ne pas être ni cette chose ni cette autre.

X ou Y = non (ni X ni Y).

Par exemple, être vert ou bleu, c'est ne pas être ni vert ni bleu.

Ne pas être une chose ou une autre, c'est ne pas être cette chose et ne pas être cette autre chose.

Non (X ou Y) = non X et non Y.

Par exemple, ne pas être vert ou bleu, c'est ne pas être vert et ne pas être bleu.

Ne pas être une chose et ne pas être une autre chose, c'est n'être ni cette chose ni cette autre chose.

Non X et non Y = ni X ni Y.

Par exemple, ne pas être vert et ne pas être bleu, c'est n'être ni vert ni bleu.

Être soit une chose soit une autre, c'est être cette chose ou cette autre et ne pas être cette chose et cette autre.

Soit X soit Y = (X ou Y) et non ( X et Y).

Par exemple, être soit vert soit bleu, c'est être vert ou bleu et ne pas être vert et bleu.

*

La communauté est le fait d'avoir la même chose.

Un ensemble est une chose faite de la totalité de certaines choses ayant au moins quelque chose d'identique (ou en commun).

Par exemple, l'ensemble des pommes rouges est fait de toutes les pommes qui toutes sont rouges.

Par exemple, il ne peut pas y avoir un ensemble des crayons rouges et des clés métalliques, mais il peut y avoir un ensemble des choses étant dans tel tiroir (dont des crayons rouges et des clés métalliques).

Un élément est une chose ayant d'identique (ou en commun) ce qui en fait faire une chose dans un ensemble.

*

Un type est un ensemble de choses identiques ou qui ont beaucoup d'identités.

Une occurrence est un élément d'un type.

Une occurrence d'un type est une autre chose qu'une autre occurrence du même type, mais est identique à elle.

Par exemple, soit deux chaises identiques, ces deux chaises sont deux occurrences d'un même type de chaise.

Par exemple, soit deux chaises différentes, elles ne sont pas du même type, mais elles peuvent être fabriquées avec le même type de bois: pas avec les mêmes planches, mais à partir de la même espèce d'arbre; si elles étaient fabriquées avec la même occurrence de bois, cela consisterait à fabriquer la seconde avec les mêmes planches que la première.

L'altérité d'un type implique sa différence.

Par exemple, une autre couleur (une couleur autre) est une couleur différente: si ma voiture est d'une autre couleur que celle de mon voisin, elle est d'une couleur différente.

La diversité est le fait d'y avoir plusieurs choses différentes.

La diversité est le fait d'y avoir plusieurs types de choses.

Par exemple, dans une usine où on fabrique des voitures identiques (plusieurs types de voitures), on fabrique diverses voitures; et dans une usine où on ne fabrique que des voitures identiques (un unique type de voiture), on ne fabrique pas diverses voitures.

*

Une structure est l'ensemble des relations entre les éléments d'un ensemble.

La fractalité est le fait pour un ensemble d'avoir des éléments ayant la même structure que lui.

La fractalité est le fait pour un ensemble d'avoir des éléments ayant une structure identique à la sienne.

*

Une homologie est une identité entre des choses qui est causée par une relation causale d'existence entre ces choses.

Une analogie est une identité entre des choses qui n'est pas causée par une relation causale d'existence entre ces choses.

Par exemple, la ressemblance extérieure de la baleine et des poissons n'est pas causée par un ancêtre commun aux poissons et aux mammifères: c'est une analogie.

Tableau analogique:

Par exemple, les ailes de l'oiseau et les élytres de l'insecte, qui permettent à ces deux animaux de voler et ont donc la même fonction, sont analogues et non homologues, car leurs ancêtres communs étaient des animaux sans aile ni élytre, rampant et non volant.

Tableau analogique:

Par contre, il y a homologie entre la nageoire du poisson, la patte du reptile et l'aile de l'oiseau.

Tableau homologique:

*

La dépendance est le fait pour une chose de pouvoir être modifiée, changée par (la modification d')une autre.

La dépendance est le fait d'être fait par autre chose.

Par exemple, la météo qu'il a fait hier ne dépend pas de ce que je fais maintenant.

L'interdépendance est la dépendance réciproque.

*

Un système est un ensemble dont les éléments sont interdépendants.

Un système est un ensemble dont chaque élément peut modifier ou être modifié par les autres éléments.

Un système est un ensemble où la modification d'un élément peut causer la modification d'autres éléments.

Un système est un ensemble dont chaque élément existe selon l'existence des autres éléments de l'ensemble et selon sa structure.

Un réseau est un système.

*

L'interaction est le fait qu'un facteur n'a pas le même effet lorsqu'un autre facteur intervient: les facteurs n'ajoutent pas leurs effets, ils se modifient réciproquement.

*

Une propriété holistique (ou émergente) d'un système est une propriété qui est causée par la structure ou les relations des éléments de ce système mais qui n'appartient à aucun des éléments du système et ne peut être causé que par la somme des propriétés des éléments du système.

Par exemple, la structure et les relations des molécules d'H₂O cause la liquidité de l'eau mais aucune de ces molécules n'est en soi liquide.

Par exemple, il n'y a pas d'holisme dans le fait qu'un mur de briques soit rouge parce que ses briques sont rouges (le mur étant un ensemble de briques rouges); par contre, il y a holisme du rouge du mur et des briques relativement aux atomes qui composent le mur et les briques (le mur et les briques étant des ensembles d'atomes).

*

La transitivité est le fait pour une relation que, s'il y a cette relation entre une chose et une autre, et la même relation entre cette autre et une troisième, il y a cette même relation (dans le même sens) entre la première et la troisième.

Par exemple, l'égalité est une relation transitive (si A = B et B = C, alors A = C), les relations de grandeur (plus grand que ou plus petit que), d'antériorité, de postériorité, d'implication, de parallélité sont transitives.

Par exemple, l'inégalité est non-transitive (si A ≠ B et B ≠ C, alors A = C ou A ≠ C), la perpendicularité.

Par exemple, la maternité et la paternité sont anti-transitives (si A est la mère de B et B est la mère de C, alors A n'est pas la mère de C).

*

L'ordre est le fait pour un ensemble d'avoir ses éléments réunis en sous-ensembles séparés les uns des autres, ou réunis par une relation transitive (ou par deux relations?).

Par exemple, un placard de vêtements ordonnés est un placard où les chaussettes sont mises dans un même espace, les pantalons dans un autre espace, les chemises dans un troisième, etc.

Par exemple, on ordonne un ensemble de personnes par leur grandeur si on les aligne du plus petit au plus grand, de gauche à droite: X étant plus petit que Y, X est placé à gauche de Y.

Le désordre est le fait pour un ensemble de ne pas avoir ses éléments réunis en sous-ensembles séparés les uns des autres, ou réunis par une relation transitive.

*

Un groupe est un ensemble d'éléments réunis par une opération de composition telle que, appliquée à des éléments de l'ensemble, il en résulte un élément de l'ensemble, et où il y a un élément neutre tel que composé avec un autre il ne le modifie pas, où il y a une opération inverse telle que, composée avec la première opération, il en résulte l'élément neutre, et tel que les compositions sont associatives.

Par exemple, le groupe des nombres entiers positifs et négatifs est réuni par l'opération de l'addition avec le zéro comme élément neutre (n + 0 = 0 + n = n) et comme opération inverse la soustraction (+ n - n = - n + n = 0), et les opérations y sont associatives ([n + m] + l = n + [m + l]).